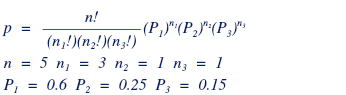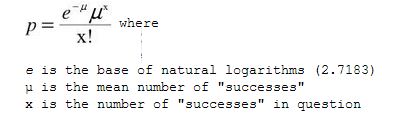The Multinomial and Poisson Distributions

As you and your friend travel one thousand miles to watch a series of Barclays Premier League football, the two of you deliberate the probability distributions for the possible results over the five game series. Conversely, it hits you right in the face, at MDM4U in school, you learnt calculating probability distributions for binomial circumstances, but football always encompasses a draw. You could manipulate the probabilities and count a “draw” as a loss, but would that really be a representative probability distribution? Undoubtedly not, unless you or your friend were rooting for one team so badly, that any result against them counted as a loss.

In class, Bernoulli trials in connotation with binomial distributions were conferred. As a reminder, let us take the time to revisit Bernoulli trials and binomial distributions. Bernoulli trials are recurrent, independent, indistinguishable trials measured in terms of success or failure. Several examples of independent trials include tossing a coin one hundred times, rolling a pair of dice, or pass and fail situations.  Binomial distributions are probability distributions where a definite outcome is anticipated, and where there are two possible results; success or failure. The probability of success is denoted as p, while the probability of failure is denoted as q. The sum of these two probabilities, must, in all situations be equal to one.  Let us take an example; what is the probability of tossing exactly three heads out of five tosses? The first step is to determine the success and failure, along with the probabilities and desired number of successes and failures, respectively. Therefore, the probability of achieving exactly three heads in five tosses is 0.3125 (10/32).

Going back to the football example, the situation of a draw is not covered by a binomial distribution, so, what do we do? Instead of using the binomial distribution, where there are two outcomes (success and failure), we proceed to using the formula for multinomial distribution, which allows infinite (n) outcomes, as long as the probabilities for (n-1) outcomes are defined, and the number of desired outcomes are also defined.  Suppose you were attending the game series between Chelsea and Manchester United, the probability of Chelsea winning is 60%, while the probability of Manchester United winning is 25%. The probability of a draw is the remaining 15%. If the series was five games long, what is the probability of three Chelsea wins, one Manchester United win and one draw? And what is the number of expected Chelsea wins, Manchester United wins and draws in the five game series?

The first step towards solving this issue is to gather the formula, and identify all the values associated with it. The formula for multinomial distributions is similar to that of the binomial distributions, with the only difference being an added outcome, denoted as “r” or “n₃”. In the football instance, n equals to five, because the game series is five matches long. The desired outcomes are three Chelsea wins (probability of Chelsea winning is 60%), one Manchester United win (probability of Manchester United winning is 25%),and one draw (probability of one match going for a draw is 15%). Subsequently, the values are to be entered into the formula and calculated based “on the order of operations”. After doing the above mentioned, the probability of Chelsea winning three games, Manchester United winning one game and one game stalemated, is attained, and is found to be 0.162 (or 16.2%).

However, only parts of your queries are answered. As a football fanatic, you still do not know how many games your team is expected to win, or how many draws are expected to be part of the series? Recall that the formula for obtaining the expected number of successes in a binomial distribution was simply n x p (where n was the number of times the experiment/event occurred, and p was the probability of success). Similarly, the expected value for the number of desired outcomes can be obtained by multiplying the number of events/experiments by the probability of the desired outcome.

In the situation of the football series, the probabilities are 60%, 25% and 15% respectively, while the number of games occurring within the series is five. As a result, the expected values for the series are three Chelsea wins, one Manchester United win, and one draw.  In summary, situations where the number of outcomes are greater than two require more than a binomial distribution, hence the multinomial distribution is an effective manner in which the probabilities for situations that include more than two possible outcomes. Similarly, the expected value can also be calculated for these situations. The multinomial distribution can easily be used in situations like chess, stock prices, sporting events, and any other situation involving more than two possible outcomes.  However, what about situations in which rates are involved?

Over a century ago, French mathematician Simeon-Denis Poisson developed, what is known today as the Poisson distribution. There are several uses for the Poisson distribution. For instance, this style of distribution can be used to approximate the binomial distribution if the value of p is miniscule, but the value of n is extremely large. However, the more common use of the Poisson distribution is when an average rate of occurrence is given. It is especially used when the mean number of successes (predetermined outcome) is given, and the probabilities of various numbers of successes are required. By definition, the Poisson distribution is a discrete probability distribution for the counts of events that occur randomly in a given interval of time (or space). The Poisson distribution only works if the events are independent. The formula for the Poisson distribution is shown below:

With regards to the Poisson distribution, the mean is equal to λ, while the standard deviation is equal to the square root of the mean.  As an example, you were tasked with  calculating the probability of observing 10 births in a given hour at the hospital, with the average rate of births per hour at the hospital being only 3. The first step is to provide a let statement, that x equals the number of births in a given hour.  Consequently, a Poisson distribution statement must be written. The general formula for that is X – Po(λ). Therefore, the general statement for this instance is X – Po(3). The mean of the births per hour at the hospital is 3, while x is 10.  After inputting all the information into the formula, you would realize that the probability of the desired outcome is 0.08%.

In summation, where the binomial distribution is unable to provide probabilities for situations, the multinomial distribution can be used when the number of outcomes exceeds two, and the Poisson distribution can be used when rates are provided, or the probability is too small and the sample  is too big to use the binomial distribution.

References:
http://www.youtube.com/watch?v=tx9wspMQvoY
http://www.statlect.com/mddmln1.htm
http://warnercnr.colostate.edu/~gwhite/fw663/MultinomialDistribution.PDF
http://www.math.uah.edu/stat/bernoulli/Multinomial.html
http://onlinestatbook.com/2/probability/multinomial.html
http://ncalculators.com/math-worksheets/poisson-distribution-example.htm
http://ncalculators.com/statistics/poisson-distribution-calculator.htm
http://easycalculation.com/statistics/learn-poisson-distribution.php
http://www.stats.ox.ac.uk/~marchini/teaching/L5/L5.notes.pdf
http://onlinestatbook.com/2/probability/poisson.html

Poker: 100% Skill & Numbers and 50% Luck

Walking into a casino, you may have told yourself the following: “winning and losing at a casino is solely dependent on luck”. On the contrary, success in most card games at the casino is split between luck and your competencies at understanding numbers. For all it may be, poker, whether five or seven card, whether one or multi deck is a number’s game.  Anthony Holden, the author of Big Deal once said “The good news is that in every deck of fifty-two cards there are 2,598,960 possible hands.  The bad news is that you are only going to be dealt one of them.”

With poker, a common misconception is that the more decks that are involved, the harder the chances of winning. That, for the most part, isn’t true. When gambling, the higher the odds you receive, the lower the probability of the desired events occurring.  Gambling odds are not odds in favor, but instead are odds against, which is the probability of the event not occurring divided by the probability of the event occurring. This entry aims to a) derive the odds pertaining to each hand in five card poker with one, two, three, and four decks being involved and b) articulate the different probabilities that arise when dealing with single and multiple decks, namely, two, three and four decks.

To begin with, let me take the time to explain five card poker (often referred to as “five card draw”), which includes a dealer. Each player, including the dealer is dealt out five cards. Your goal is to have a hand better than the dealer’s. There is only one round of gambling (in most cases), which occurs before the hand is dealt. You can put as much money on the table, and should you win, the payout will be your money multiplied by the odds predetermined by the casino. After receiving your hand, you have the choice of exchanging a maximum of three cards for a maximum of three cards, dealt directly from the deck. Should you have a hand better than the dealer, e.g. four of a kind vs. two pair, you win your bet against the dealer, and will be paid the odds of a four of a kind multiplied by the amount of your bet.  Before I lose you as a reader and this entry progresses, it is vital that you understand the types of hands involved in poker.

Consider this scenario, you are playing poker in an underground den with one deck, amongst your five card hand; you have five spades, albeit in no definite order, your cards are A, 3, 6, 9, Q. You do not have a straight, but, your hand ensures that the probability of obtaining a royal flush inches closer to zero for everyone, including the dealer. The dealer says that you are allowed to bet during the game. The odds of you winning are substantially higher now, because there are only four types of hands that are superior to yours, but the probability of obtaining those hands are very remote and you can bet during the game. As a result, you may choose to raise the dealer, because your chances of winning are higher. By understanding the numbers well enough, you can make an informed decision whether you wish to raise, call, or, fold versus the dealer.  The table below shows you the approximate probabilities and odds for each type of hand in five card poker with one deck.

Mathematical Reasoning:

After seeing how the probabilities, and odds for each possible hand in five card poker with one deck was derived, the comparison of probabilities between one deck and multi deck five card poker will be shown in the following table.

As you can see from above, the probabilities of achieving most hands increases as you add more decks. Apart from straights and high cards, the probabilities of each of the hands increase, while the odds decrease. Yes, the payout odds for each of those hands also decrease, but there is a greater chance of you winning. So, what type of gambler are you, a greedy one bent on making the most amount of money, or a smart one content with just winning?

So, walking into a casino, will you still tell yourself the following: “winning and losing at a casino is solely dependent on luck”.  I certainly hope not because in most card games at the casino or even in your hidden gambling ring, success between luck and your competencies at understanding numbers. If you know the numbers and are allowed to make bets during the game, you may have a significant advantage over your opponent. The next challenge for you, as a reader or as a gambler would be to identify whether playing poker which involves larger hands (e.g. six card, seven card, etc.) increases your probability of winning. Poker, be it five or seven cards, is in large part a number’s game.

Phil Hellmuth once said, “I guess if there weren’t luck involved, I’d win every time”. He mastered the game of poker, ensured that he lost little, but still could never win a hundred percent of the time. It is often said “when a man with money meets a man with experience and skill, the man with the skill and experience leaves with the money and the man who had the money leaves with experience and skill”.

References:
http://wizardofodds.com/games/poker/
http://blog.contextures.com/archives/2009/01/16/calculate-a-ratio-in-excel/
http://www.math.hawaii.edu/~ramsey/Probability/PokerHands.html